To your second point I personally try to avoid using either cc7 or cc11, I prefer to use velXF for expression and daw faders or mirpro for orchestra balance. However it’s all fine to use cc’s for either purpose and honestly it’s not that critical that You get the exact gain back through some other means after synchron, if you want to bump the level back up equally across all your synchron instruments so that the orch balancing will be retained then send them all to a bus, add some gain back until it’s in the zone you want. Doesn’t have to be precise really. All this talk about DB’s has been a side show that complicates the matter more then it needs to

Dewdman42, I'm going to stand by empirical evidence. Empirically, I found that your solution does not work.

The simple tests I did on your solution produced a result that speaks for itself and can very easily be reproduced and inspected by others. If you would kindly address that result, I'd welcome your explanation of it.

What result did you want me to respond to? As I said already, the discussion about DB’s on this thread is clouding the topic unnecessarily

With this extremely basic test, anyone still in any doubt can and should try this:-

With Master Volume set a max, start some sustained sound going forever. Pump up Synchron Player's output by any method until it's just tickling 0 dBFS on Synchron Player's output meter. Then drop Master Volume to half way, at CC level 64.

What do you read on the output meter? Is it about -6 dBFS,  as the spreadsheet says it should be? Or does it actually read about -12 dBFS, as predicted by Macker's figures? (Spoiler: it'll actually read about -12 dBFS)

It's ok Dewdman42, I don't need an answer from you because the empirical facts speak loudly and clearly without any help. Anyone can run this very simple test and see for themselves. It's really not rocket science.

Paolo, so, we're back at the original problem - we haven't provided you with any real help. Shame on us, lol.

Yeah I can see the 'twin-track' method ought to work as your compensation trick, as long as your instrument presets all provide just enough room for raising your "natural balance' fader by the amount you require (about 2.5 dB, looking it up in my table). And I reckon it could be done just by comparing the two loudness levels carefully by ear, or by by whatever meters happen to be there - without any need for fancy metering. 

One thing I'm thinking is, wouldn't it eventually get a bit tedious for you? If so, would it be less hassle to insert a VSL gain plugin on all active channels in the Sy Player mixer, and raise them all by that 2.5 dB for your compensation? Up to you of course - whatever method you're most comfortable and confident with.

Hello Hermann and welcome to the forum.

Looks like you prefer to dive into the deep end - great stuff! lol

Appreciate your testing and your kind comments about my tests and calculations. Totally agreed about empirical evidence being the ultimate arbiter. Heaven knows we need more of that!

The ultra simple test you describe is indeed a deal-breaker. No need for lengthy confabulations or endless faffing with these or those conditions for further tests. That one test will tell the truth clearly without fear or favour.

Good job! 

@Another User said:

What do you read on the output meter? Is it about -6 dBFS,  as the spreadsheet says it should be? Or does it actually read about -12 dBFS, as predicted by Macker's figures? (Spoiler: it'll actually read about -12 dBFS)

You are unfortunately still missing the part about reference level.  Macker also appears to be missing this component.  The spreadsheet, as well as the other website I quoted, are referring to the amount of attenuation, not the predicted meter reading.  The source content you are using for a test has an unknown reference level.  

But it doesn't matter that you don't know this, the spreadsheet and the website tell you how much attenuation is being applied by Synchron..and you can then use the same amount of DB + gain to bring it back.

I am basing this on well understood mathematics bout dBFS and amplitude conversion, I'm not making it up.  Hey I'd like to know if this math works too...  I will try a test....

@Macker said:

Paolo, so, we're back at the original problem - we haven't provided you with any real help. Shame on us, lol.

Actually, it's a very interesting discussion, with some math that is useful to learn. But a clear answer (at least, not one I can grab) doesn't seem to be there, yet.

An empirical solution has the advantage of living in our main domain – the music/sound dimension. This one, we can easily understand!

Paolo

@PaoloT said:

Actually, it's a very interesting discussion, with some math that is useful to learn. But a clear answer (at least, not one I can grab) doesn't seem to be there, yet.

 

oh wait...I thought we figured that out already.  What is the open question exactly?

So I did a simple test.  

1. measure a Synchron instrument with CC7/CC11/CC1 all set to max, write it down.
   
   
2. set CC11 = 110, measure again.
   
   
3. add a trim plugin after Synchron and fiddle with different gain settings until the measured result is the same as step#1 above.

A couple points.  Its hard to be precise with this test because we have to rely on a Synchron instrument as the test sound, which is applying unknown humanization to the sound which may or may not produce consistent results.  By playing at least a dozen notes at the same velocity and keeping track of the max peak during that time..might be ok enough.

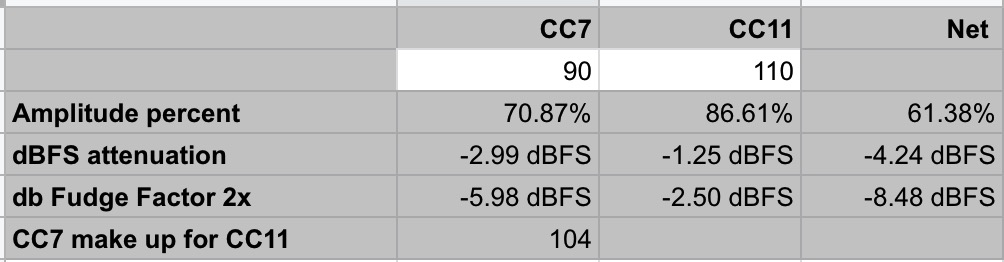
I agree with Macker that the amount of gain needed to bring the level of step#3 back to the level of Step#1 required is around 2.5db 

which is not the same value as indicated by the 20*log10 formula, which comes up with -1.25db (note - the fact that its pretty much exactly 2x of the calculated value is interesting also)

So there is definitely something more to the story, but at the moment, I'm not sure what, I think its probably that none of us, including myself are calculating reference level into it properly while doing that math.  

VSL has already stated very clearly that the CC controls are a simple percentage of amplitude.   The formula I mentioned absolutely *IS* the correct formula for converting amplitude percentage to dBFS.  But it doesn't match the measured results, I agree.

The good news is, following an attempted insurrection by the crude forces of dogmatism, modern science has reasserted its long-term possession of certain territory in the field of audio engineering,

The bad news is that the attempted insurrection happened at all, and here in VSL's forum.

In the Mac's dictionary, "dogmatism" is defined as "the tendency to lay down principles as undeniably true, without consideration of evidence ..."

Over the past 5 centuries, modern science has shown the value that empiricism brings to the progress of human existence. Do we want to turn the clock back to pre-modern times, when often absurd dogmas ruled the roost pretty much across the board? I don't think so. Do we appreciate attempts to drag us back there? I don't think so.

So I'll just say this. Let's be careful who we listen to and believe, and let's make sure that the long-established value and reputation of empiricism in the disciplines of mathematics, science and engineering are protected and upheld against any who try to cast them aside imperiously as if mere trash. Also there are further offences to watch out for and guard against, such as bush-league sophistry and smearing tactics, as used since time immemorial to pave the way for, defend and promote dogmatism.

Over and out.

@Dewdman42 said:

oh wait...I thought we figured that out already.  What is the open question exactly?

It's still the one I asked in the first post. Many interesting ideas and solutions in this thread, but not yet one looking as effective as working with a vu-meter!

Paolo

@PaoloT said:

A practical answer to myself to get the same default 'natural' balance of the presets when lowering Expression from 127 to 110

I compared the original VSL presets and my custom ones, whose Master Volume was recalculated by multiplying the original value by 115.3%. It works! Probably just by chance, but the level are matching for all the presets.

Paolo

@PaoloT said:

A practical answer to myself to get the same default 'natural' balance of the presets when lowering Expression from 127 to 110

I compared the original VSL presets and my custom ones, whose Master Volume was recalculated by multiplying the original value by 115.3%. It works! Probably just by chance, but the level are matching for all the presets. Paolo And the Vu meter approach has been mentioned several times in the thread as an additional solution. So it seems you are in fact resolved. What other solution could there be? What is left unresolved? Using approximately 115% to compensate cc11=110 is right in line with the calculations I gave you earlier ( now on the spreadsheet ) . The cc11=110 is 86.61% of full. If you take 1/.8661 you get 1.15 which is 115%. Your Vu measurements confirm this. You can change cc11 to any other value instead of using 110 for home and use the calculation 1 / ( cc11 / 127 ) to obtain the needed compensation to use for cc7 fader as a percentage. But when in doubt, using meters to get it where you want is also perfectly fine way to get it without trusting math

@Dewdman42 said:

right in line with the calculations I gave you earlier

Not that I pretend any merit, but it's the formula I proposed in the fifth post of this thread. I only needed confirmation with the most accurate measurement I could do.

I don't really get this idea of "it's resolved, so what's that you still want?". The process is more interesting than the pure result.

Paolo

Sorry I am not meaning to stop any further discussion just checking to see whether you got past your original question which it seems like you did. I also did not mean to offend you by suggesting some math to use or to add my own thoughts about how to derive this number accurately. I hope that anything I have said has been helpful in some way, otherwise this thread has become toxic and I intend to leave it. Just wanted to make sure your question has been answered and i think it has been answered at least four different possible solutions. Cheers

@Dewdman42 said:

I hope that anything I have said has been helpful in some way

Absolutely yes, and thank you very much for this! You brought several interesting things to this articulate discussion!

Paolo

Paolo, the error exposed in the spreadsheet has some far-reaching consequences. You may or may not understand the theory behind this, but at the very least you do need to be aware that the erroneous thinking behind that error in the spreadsheet put the discussion on the wrong footing right from the start.

If you'll forgive the techie tedium, I'll go through it one more time.

The formula 20*log(CC ratio) originally (and wrongly) used for the spreadsheet is applicable ONLY IF the CC ratio (perhaps expressed as a percentage) determines audio level changes produced by a device according to what's called a linear law (also known as a straight-line law). That is to say, where a linear law applies to a specific CC-controllable device, any given % change in CC value on the device's input, will cause the same % change in audio level at the device's output. But in the case of volume controls, such as Sy Player's Master Volume and Expression faders, we know from my measurements that they don't work according to a linear law. And that's no surprise at all, because in fact volume controls are always physically manufactured (and now digitally modelled in software) to have what's called a logarithmic law. That's been the general rule as far back as the earliest days of electronics, and it's to match the fact that our ears (and certain other senses also) respond to stimuli in a physiological way that happens to be pretty close to mathematical logarithmic functions, as first described by Ernst Weber and Gustav Fechner in 1860.

The 20*log(ratio) formula is used to express voltage ratios as decibels. The standard definition of the decibel  specifies power ratio, not voltage ratio, and dB are defined as 10*log(power ratio). However, as long as impedance remains a constant, it can be shown that power is directly proportional to voltage squared. And in the magical world of logarithms, multiplying the log of a number by 2 is the same as squaring that number before converting the result to a logarithm. So we multiply the power-decibel formula by 2, and arrive at 20*log(voltage ratio). And in practice the result of the 20*log(voltage ratio) formula is sometimes expressed as dBV. Why voltage? Because voltage (in a well designed audio system) is directly proportional to the resulting sound pressure (units of which are called pascals, defined as Newtons per square metre), which is what our ears respond to. And because of this direct proportionality between voltage levels inside the sound system and the resulting sound pressures eventually produced in the acoustic domain, dB SPL (Sound Pressure Level) are used in the same way as dBV are used in the electronic domain, i.e. using 20*log(sound pressure ratio) to express audio level changes. In practice, dB SPL is always referenced to the threshold of human hearing, conventionally defined as 20 micropascals. And today, inside digital sound systems, instead of audio voltages we have numbers that are directly proportional to the voltage eventually produced by the digital-to-analogue convertor in the system's output stage. So the 20*log(ratio) formula still applies in digital sound systems, just as it did in the days of analogue mixing boards. Moreover, dBFS ("FS" = full scale) is merely the most convenient way to express an absolute level inside the sound system; in fact a ratio is still involved, but in this case the level of interest is referenced to the Full Scale level inherent in the system - regardless of whether the system is analogue or digital. It is customary to express attenuation or gain amounts as simply dB, not as dBFS, because for attenuation and gain, usually it is the ratio which is of interest, not the absolute level.

 

Now let's consider further the ratio part of 20*log(ratio). If we move the Master Volume slider from full scale (127) down to half scale (64), obviously we can call that a ratio of 0.5 or 50% in relation to the full scale setting on the device's input. But does that result in a 50% change in sound level on the output of this volume control device? No, it most certainly does not, as is verifiable by watching SyPlayer's output level meter, and from my graph and table of input/output measurements. If the sound level dropped from 100% to 50% we would expect to see a fall of 6dB in the output meter reading. But in reality  the sound level falls by 12dB. My 40*log(ratio) formula is simply a reasonably valid mathematical model of these faders, according to my measurements. The factor of 2 above the usual 20*log(ratio) expression is due to the inherent scaling of the logarithmic law of the fader devices. Calling it a "fudge factor" is merely admitting inability to understand the underlying mathematics, as well as an attempt to deflect attention from the fact that the original formula incorrectly assumed a linear law.

From what I've read in the thread - some of which I see has been subsequently edited - you've been advised all along to treat the two volume faders as if they were linear-law devices. I have added my advice that it may be possible to get away with this incorrect assumption just so long as very small changes of ratio are involved. But more generally, I don't see that there's any quick, easy or convenient way of working around the mathematical ramifications of the logarithmic law of these two faders, regardless of whether we express the output audio level changes as dB or as simple ratios. That said, logarithms and decibels owe their existence to their mathematical convenience. For example in working with audio, we can just add or subtract decibels, pretty much in the same quick and easy way as when, say, we do cash transactions in the grocery shop. As far as I know, nobody's invented or discovered a way of making things even more convenient than using those simple additions and subtractions.

My conclusion is that the goal of ignoring the log-law of the fader devices and getting away from decibels, is, sorry to say, just pie in the sky.

Well this dreadfully long lecture probably hasn't served to simplify or clean up the awful mess this thread got into. But I had to put it out there in the hope that, with any luck, nobody else will be led up the garden path by those very wrong technical assumptions and principles posted in this thread.

Macker you are the one that has dragged this discussion into the gutter with your endless blathering and accusing about how stupid you think other people are. Unless you are making your measurements outside of the box using sound pressure meters or actual voltage meters, the stuff you just outlined is irrelevant. Digital audio workstation use dBFS as a measurement and the calculation from amplitude percent to dBFS is as I have said: 20 * log10 ( amp percent ) There are are no actual electronical faders involved here nor passage of sound through the air as sound pressure in these measurements. I still do not see a clear explanation for the 2x factor from there, but I don’t disagree with your measurements either as i have measured the same. I don’t claim, as you seem to, to be any kind of expert on these matters I am simply responding to the thread. I still can find no explanation for this 2x increase above the standard dBFS calculation. If you know the correct answer and can share it without turning it into an offensive personalized attack and drivel I would be interested to hear it and can then relabel the spreadsheet with a better label then “fudge factor” to avoid your scorn. but I don’t think you truly do know the answer you are just blowing around a lot of irrelevant material that is not really helpful. As I said from the very beginning and you attacked with impunity, the fader in synchron is stated by VSL thus far to be applying a simple linear attenuation on a percentage scale. I understand that you would like to see them label the fader with the equivalent db attenuation on its logrithmic scale so perhaps you can make a simple feature request rather then dragging me and everyone else on this thread through the gutter pontificating your expertise about DB’s and offensive accusations. I still do not find a reasonable explanation yet for why this linear fader produces 2x of calculated dBFS. And I would be interested to know but this is seriously my last post on this thread because primarily you have made it very unfriendly, very toxic and way more work then it needs to be. I also don’t particularly think synchron is in “dire” need of db labels on the GUI, but it’s also not a terrible idea. In the meantime I hope the calculations in the spreadsheet can help you or others to quickly calculate the effective attenuation expressed as DB’s.